Prefix Sum is a simple and efficient approach to calculate sums of elements of any contiguous subarray in constant time. But what if you want to update an element in the array. Now it takes O(n) to do that. Is there a way to do it faster?
Motivation
Sometimes a task arises to compute sums over contiguous subarrays. The prefix sum is a perfect solution for that in case the initial array is static. But what if we want to update some elements of the array? In this case we’d need to update the prefix sum array as well. In the worst case it’d require to update all elements. So the time complexity of such operation is $O(n)$. A Fenwick Tree, or a Binary Indexed Tree is a data structure that allows to reduce the time complexity of the update to $O(log(n))$. The downside is that computing a sum of a subarray becomes $O(log(n))$ as well.
How Fenwick Trees Work
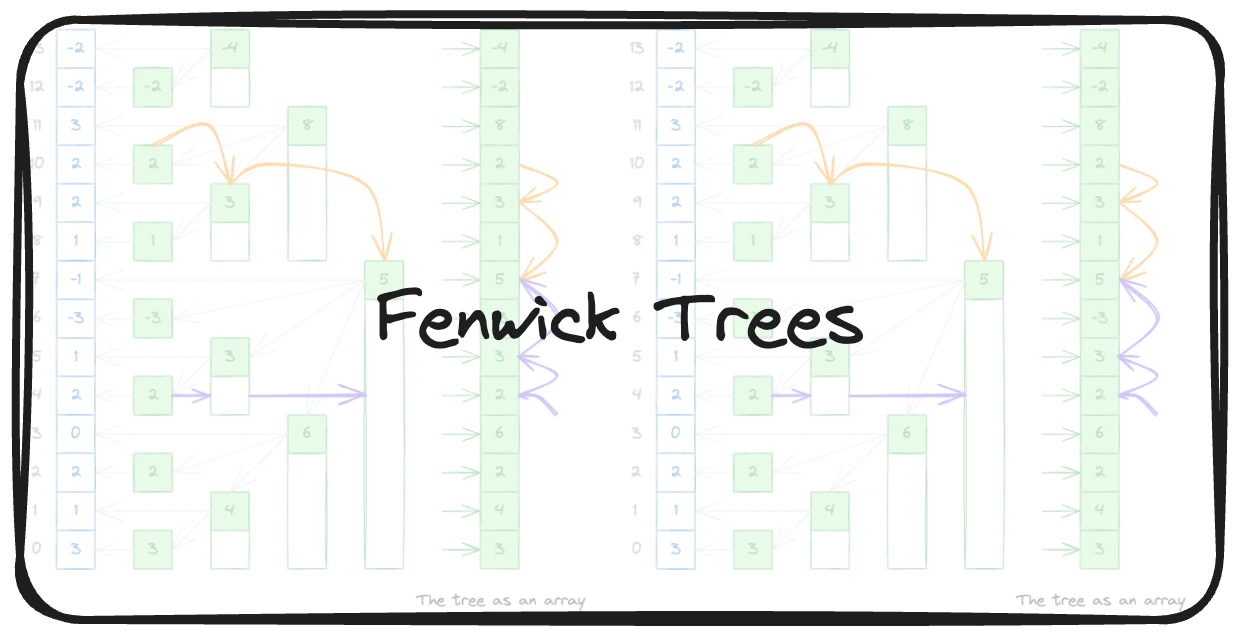
Suppose there is some array. On the picture below it’s colored with blue and the indices are colored with gray. Imagine sending signals along the initial array (denoted with green rectangles). The length of a signal is always a power of 2, and it never changes. When a signal ends it’s absent for the same length as it’s length and then it starts again. Signals of varying lengths start at index $0$, and they spread until the end of the array.
For example, as it’s illustrated on the picture below, signals of length $1$ start and end at indices $0, 2, 4, 6, 8, 10, 12$. Signals of length $2$ occupy indices $[0, 1], [4, 5], [8, 9], [12, 13]$. Signals of length $4$ occupy indices $[0, 3], [8, 11]$. And the signal of length $8$ occupies indices from $0$ to $7$.

Each signal stores the sum of the values the signal corresponds to. For example the biggest signal on the picture stores the sum of indices from $0$ to $7$ which is $3+1+2+0+2+1+(-3)+(-1) = 5$. The signal at indices from $8$ to $11$ stores $1+2+2+3=8$.
Notice how each signal ends at a different index. This allows us to store the tree in an array of the same length as the initial array.
Calculating Sums of Subarrays
Now if we want to calculate a sum of the first $N$ elements in the array we can sum the biggest signals that cover all the indices. For example to find the sum of elements at indices $[0, 10]$ we can sum signals at indices $[10, 10]$, $[8, 9]$ and $[0, 7]$. Orange arrows illustrate that.
To calculate the sum of an arbitrary subarray $[M, N]$ we just calculate the sum of $[0, N]$ and subtract the sum of $[0, M-1]$ from that.
$$ sum([M, N]) = sum([0, N]) - sum(0, M-1) $$Visually it’s easy to see which signals we need to sum. But you might be wondering how to find them programmatically. And there is an easy way to do that. Given an index i the next index to jump to can be calculated this way:
where $\&$ is a bitwise AND operator.
For example:
$$ 10 \& (10+1) - 1 = 9 $$$$ 9 \& (9+1) - 1 = 7 $$$$ 7 \& (7+1) - 1 = -1 $$Once we get to $-1$ we know we need to stop.
Updating the Tree
In order to update an element in the tree we need to update all the signals it’s contained in. For example the element at the index $4$ is contained in the signals at indices $[4, 4]$, $[4, 5]$ and $[0, 7]$. See purple arrows.
As previously it’s easy to see visually which signals we need to update. But how to identify them programmatically? It turnes out there is also an easy way to calculate indices for the updates. Given an index i the next index to update is:
where $|$ is a bitwise OR operator.
For example:
$$ 4 | (4 + 1) = 5 $$$$ 5 | (5 + 1) = 7 $$$$ 7 | (7 + 1) = 15 $$$15$ is out of bounds of the array, so we know we need to stop the updates.
Building the Tree in Linear Time
It’s easy to see that we can construct the tree in $O(n\ log(n))$ time: iterate over the initial array and for each element add it to the signals at indices calculated with $i|(i+1)$ formula.
But notice how a smaller signal is always contained in a bigger signal. For example the signal $4$ is contained in the signal $5$ and the signal $5$ is contained in the signal $7$. We can utilize this knowledge in the following way: when we are done with calculating the signal sum we can add it right away to it’s bigger signal.
Conclusion
Fenwick Trees is a data structure that most likely you won’t use too often, but it might come in handy sometimes. Just remember how to calculate indices for both the sum and the update operations and know that the tree can be constructed in linear time. I find this data structure beautiful in some sense and I enjoyed learning about it a lot.